|
Hosted by the courtesy of GitHub |
The stars ASAP



 Durée du voyage intersidéral  Résolutions de l'ONU en HTML  Bussard Ramjet 
 |
DWARF : dwarf2xml
 ELF : libelf examples  Code presentation : ctoohtml  |
|
Hosted by the courtesy of GitHub |
The stars ASAP



 Durée du voyage intersidéral  Résolutions de l'ONU en HTML  Bussard Ramjet 
 |
DWARF : dwarf2xml
 ELF : libelf examples  Code presentation : ctoohtml  |
Translation : Emmanuel Azencot Author : Emmanuel Azencot Creation : Fri May 2 16:13:44 CEST 2014 Update: Fri May 2 16:13:44 CEST 2014
Mouvement d'autres bussards ramjets |
 |
Mouvement du bussard ramjet idéal |
Le voyage intersidéral est, encore aujourd'hui, un pur exercice théorique. Il est hors de notre portée technologique en ce qui concerne le transport d'humain. Les solutions, même théoriques, qui fonctionnent ne sont pas légions. Ici donc, il ne s'agit que de théorie et de calculs dans des cas idéaux.
Le bussard ramjet, décrit dans son principe par le Dr Bussard [1], prélève de la matière sur le milieu pour satisfaire les besoins énergétiques de la propulsion intersidérale. Cela permet de s'affranchir de la contrainte de Tsiolkovsky [2] qui s'applique dès lors que le mobile embarque le carburant qui lui est nécessaire pour accomplir son voyage.
En effet, cette contrainte interdit tous les carburants classiques y compris la fusion nucléaire. Seuls les carburant presque totalement convertis en énergie peuvent raisonnablement être envisagés. Certaines solutions, très théoriques, ont été proposées, notamment l'antimatière [3] ou les micros trous noirs [4].
Les études menées sur le ramjet du Dr Bussart montrent qu'il s'agit d'une solution trop ambitieuse [5] et que sa mise en œuvre, si elle l'est un jour, sera probablement plus lointaine que celles qui transporteront leur carburant.
Cela dit, c'est la seule qui ne soit pas soumise à la contrainte de Tsiolkovsky. Elle pourrait donner une solution pour des objectifs très lointain. C'est ce qui fait son intérêt. En effet, il ne semble que le bussard ramjet n'ait pas de limite de vitesse autre que celle de la lumière [6].
Dans la suite nous allons étudier le cas idéal ou toute la matière et l'énergie qui sont capturées sont utilisés de façon optimale et sans pertes à la propulsion. Il s'agit d'un cas simple sur le plan des calculs qui aboutit à une résolution algébrique exacte du mouvement. Ce cas marque la borne supérieure de l'efficacité du Bussard Ramjet.
Pour ce qui est de l'exactitude, sachez que le document n'a été relu par quiconque et qu'une ou plusieurs erreurs sont cachées dedans. Pour cette raison il serait très imprudent de votre part de le prendre pour correct. Je suis très intéressé par votre retour et trouverez des adresses ou me joindre sur ce site.
En maintenant en route avec :
Dans ce dispositif, très théorique, l'intégralité de l'énergie
capturée, énergie de masse et énergie cinétique, est convertie en lumière envoyée exactement dans l'axe du
mobile. Les calculs sont faits dans le référentiel du
mobile.
On va appliquer la conservation de l’énergie et de l'impulsion dans
le cadre de la relativité restreinte. On considère ces grandeurs entre
les instants propres τ et τ+dτ, correspondants, dans le référentiel de la
matière capturée, aux instants t et t +dt.
|
|
c | est la vitesse de la lumière |
|
|
|
ρ | est la densité du milieu |
|
|
|
S | est la surface efficace de capture |
|
|
|
M | est la masse du vaisseau |
|
|
|
β | est la vitesse réduite, v/c, de la matière par rapport au vaisseau. |
|
|
|
η(x) | est la rapidité correspondant à la vitesse x. Elle vaut arctanh(x), inverse de la tangente hyperbolique. La rapidité est additive, contrairement à la vitesse. |
|
|
|
m | est la masse de matière capturée. |
|
|
|
t | est le temps dans le référentiel de la matière capturée. |
|
|
|
τ | est le temps dans le référentiel du vaisseau. |
|
|
|
γ(x) | est le facteur d'échelle entre deux référentiels se déplaçant à une vitesse réduite x. Il vaut (1- x2)-1/2. |
|
|
|
γ | est le facteur d'échelle pour la vitesse réduite β. |
|
|
|
Λ(x) | est la matrice de la transformée de Lorentz pour la vitesse x, C.f (1.1). |
|
|
|
Β | Sorte de section efficace de capture, vaut ρSc / M. |
|
Entre ces deux instant le vaisseau drague une surface S dans un
milieu de densité ρ. Il balaye un volume de S dx, ou dx est son
déplacement dans le référentiel de la matière capturée pendant dτ. On
considère le 4-vecteur différence des événements (c(τ +dτ), 0, 0, 0) et
(cτ, 0, 0, 0) soit ((c(τ +dτ), 0) -(cτ, 0,)), si on ne considère qu'une
seule dimension d'espace selon laquelle se fait le déplacement. Dans la
suite, on utilisera cette
simplification.
On veut donc changer le 4-vecteur (c dτ, 0) depuis le référentiel du vaisseau vers le référentiel de la matière capturée. On utilise la transformée de Lorentz Λ(β), puisqu'ils sont animés d'une vitesse β l'un par rapport à l'autre :
| (1.1) |
|
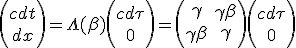
|
| (1.2) |
|
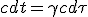
|
| (1.3) |
|
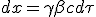
|
Le vaisseau ayant parcouru dx, il balaye un volume de Sdx dans lequel toute la matière, en densité ρ, est capturée : m = ρSdx. On remplace dx avec (1.3) :
| (1.4) |
|
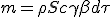
|
Le 4-vecteur d’impulsion du vaisseau, de masse M, dans son propre référentiel, et en omettant les coordonnées y et z :
|
|
|
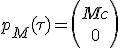
|
Pour la matière capturée, on part de son impulsion dans son référentiel que l'on transporte dans le référentiel du vaisseau animé d'une vitesse -β :
|
|
|
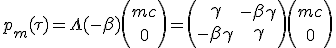
|
|
|
|
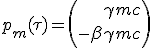
|
| (1.5) |
|
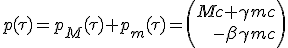
|
Toute la matière capturée m est convertie en lumière selon l'axe x, et son impulsion devient (q, -q) (1).
|
|
|
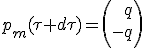
|
Comme on le verra plus loin, Il n'y a pas besoin d'expliciter q, bien que cela soit possible.
Pendant ce laps de temps, la vitesse du vaisseau a changé de dβ, ce qui lui donne la nouvelle impulsion :
|
|
|
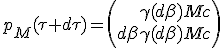
|
Comme dβ est très petit, aussi petit que l'on veut, on peut considérer que γ(dβ) est très proche de 1. En fait la mécanique classique est valable à cette toute petite vitesse et γ(dβ) ≈ 1 + ½ dβ2. On a donc un second ordre que l'on peut négliger. On obtient :
|
|
|
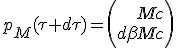
|
Le nouveau 4-vecteur d’impulsion du système est :
| (1.6) |
|
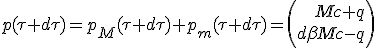
|
(1) La caractéristique des particules sans masse est que le produit scalaire de leur 4-vecteur d'impulsion par lui même est nul. Or, cette valeur, est un invariant par la transformée de Lorentz et vaut toujours m2c2.
La conservation du 4-vecteur d’impulsion résume la conservation de la quantité de mouvement et de l'énergie du système qui prend donc la forme :
|
|
|
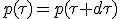
|
On peut maintenant développer et séparer les dimensions en deux équations :
| (E) |
|
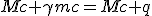
|
| (P) |
|
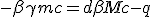
|
Et pour la matière capturée, on toujours (1.4) :
| (M) |
|
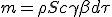
|
En ajoutant (E) a (P), puis en utilisant (M), et en posant :
| (1.7) |
|
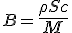
|
Il vient :
|
|
|
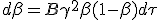
|
| (1.8) |
|
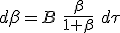 |
Ci dessous le graphe de Bβ/(1 +β), pour différentes valeurs de B : 1, 0.1 et 10 (2). Seule la partie où β ≥ 0 est à considérer.
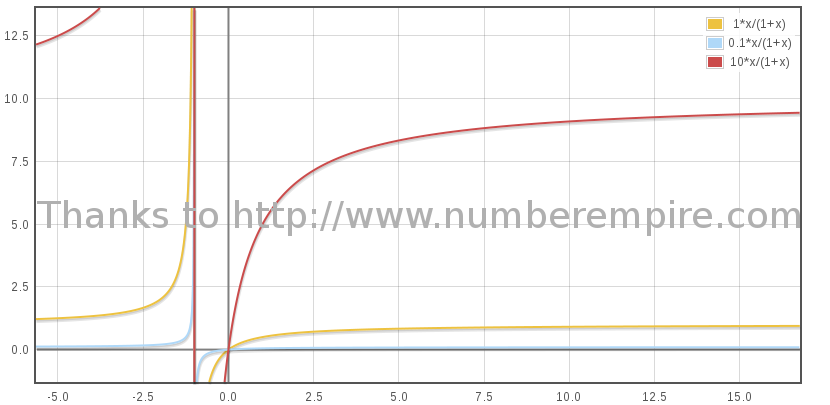
(2) Dans la réalité le rapport B est minuscule. La quantité de matière capturée dans le milieux galactique (moins de 0.1 proton/cm3) contre la masse du vaisseau, (au moins 10 000 tonnes) n'est pas vraiment favorable.
En intégrant l'équation différentielle précédente, on cherche à établir β(τ). Comme pour toute intégration, on doit fixer une condition initiale.
Quand β > 0, l’accélération est positive, donc β(τ) est une
fonction strictement croissante de τ dès que β > 0. D'autre part pour β =
0, l'accélération
est également nulle. Il faut donc un temps infini pour obtenir une
vitesse non nulle. La condition initiale basée sur β = 0, donnera un
temps τ qui tend vers -∞.
Comme β n'est pas une quantité additive, on effectue un changement de variable vers la rapidité η(β) = η = atanh(β), qui elle l'est, de façon à pouvoir intégrer. Comme la dérivée de tanh(x) en 0 est 1, on peut remplacer dβ par dη. Ainsi réécrite l'équation (1.8) devient :
|
|
|
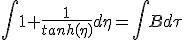
|
|
|
|
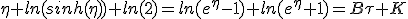 (3) (3) |
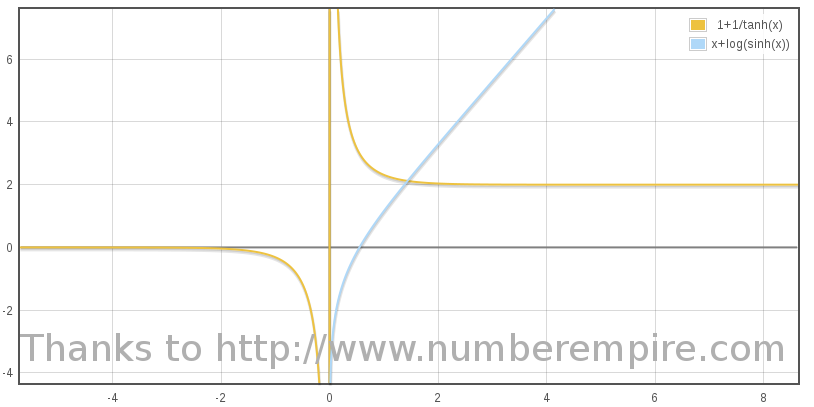
Appliquée à ce résultat, la condition initiale n'apporte pas de contraintes car quand τ tend vers -∞ la rapidité η tend vers 0, ce qui veut dire que K peut prendre n'importe quelle valeur finie. On peut choisir K = 0 pour simplifier l'écriture.
|
|
|
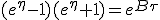
|
|
|
|
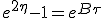
|
| (1.9) |
|
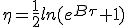
|
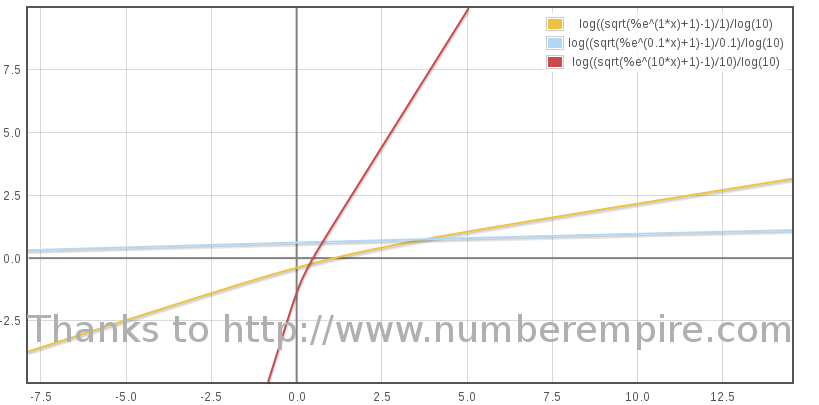
Pour τ = 0, 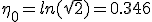 . En revenant à la vitesse réduite on trouve
. En revenant à la vitesse réduite on trouve 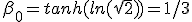 .
On en déduit que toutes les courbes de vitesse produites par les
différentes valeurs de Β se croisent à 1/3 de la vitesse de la lumière. Ce croisement se trouve être à τ = 0.
.
On en déduit que toutes les courbes de vitesse produites par les
différentes valeurs de Β se croisent à 1/3 de la vitesse de la lumière. Ce croisement se trouve être à τ = 0.
Ci dessous η(τ) pour différentes valeurs de B : 1, 0.1 et 10 :
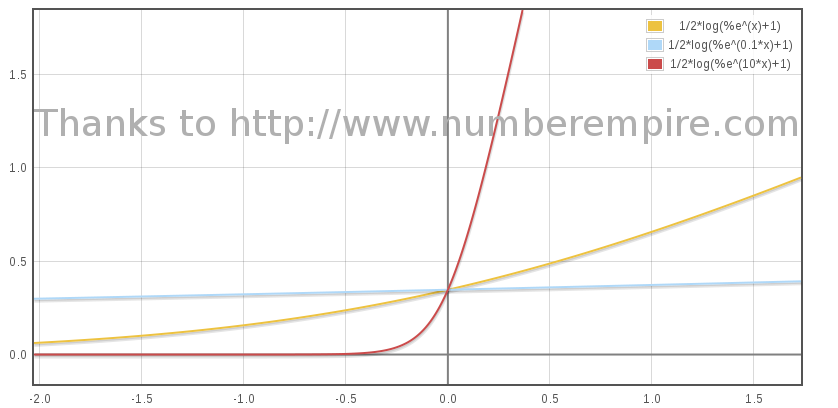
On peut maintenant calculer β en fonction de τ. Comme on l'a vu plus haut, β = tanh(η) :
|
|
|
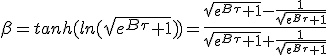
|
| (1.10) |
|
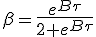
|
La limite en basse vitesse, quand τ tend vers -∞,
|
|
|
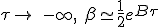
|
La limite en haute vitesse, quand τ tend vers +∞, On utilise la limite de η :
|
|
|
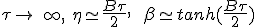
|
Ci dessous l'évolution de β en fonction du temps propre pour 3 valeurs de B :
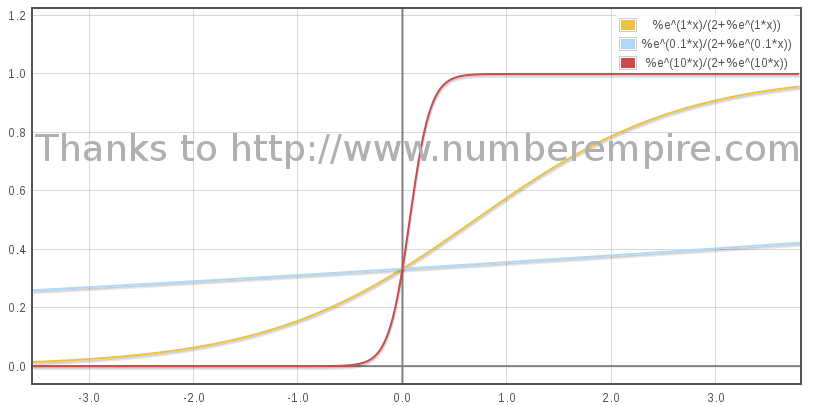
(3) Merci à Mathématica pour la première forme et à NumberEmpire pour la deuxième.
On s'intéresse maintenant à la distance parcourue par le vaisseau dans le référentiel de la matière capturée. Lors de l’évaluation de la capture entre τ et τ +dτ, on vu une expression de dx (1.3). Pour mémoire, γ = cosh(η) et surtout, βγ = sinh(η) :
|
|
|
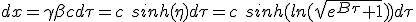
|
|
|
|
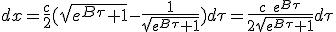
|
|
|
|
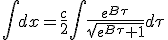
|
|
|
|
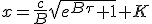
|
Quand τ tend vers -∞, x doit tendre vers 0. Il vient que K vaut -c/B, d’où :
| (1.11) |
|
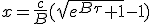
|
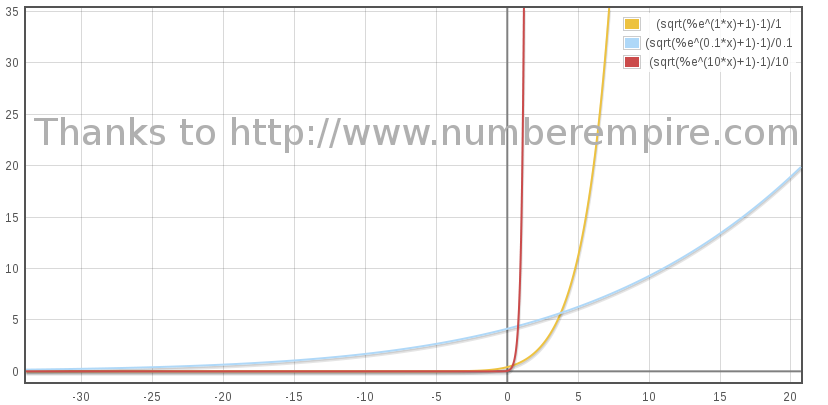
Une vue améliorée avec le logarithme de la distance parcourue :
On peut calculer la distance pour la valeur τ = 0 :
| (1.12) |
|
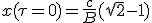
|
Un voyageur en route pour la galaxie Andromède verra la voie lactée tourner sur elle-même.
On cherche combien de temps t s'écoule dans le référentiel de la matière capturée, tout d'abord en fonction du temps τ du vaisseau. Pour cela on utilise (1.2) qui relie ces quantités. On utilisera (1.9) pour η.
|
|
|
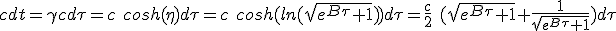
|
|
|
|
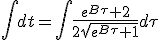
|
Grâce à Number Empire :
|
|
|
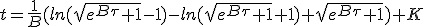
|
Pour avoir t = 0 quand τ = 0,
|
|
|
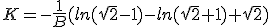
|
|
|
|
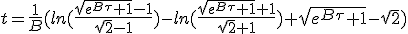
|
| (1.13) |
|
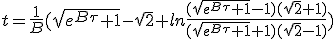
|
Évidemment, le "référentiel fixe" n'a aucun sens en mécanique relativiste, il s'agit ici du référentiel de la matière capturée, si tant est que cette matière soit elle même animée d'un mouvement homogène ce qui n'est probablement pas le cas. Compte tenu que notre soleil ainsi que étoiles proches ont une vitesse faible par rapport au milieu galactique, on peut appeler le référentiel fixe, le référentiel formé par ce milieu.
Les quantité x de (1.11) et t de (1.13) sont donc approximativement les distances et durées observées depuis la Terre. Dans le cas du bussard ramjet idéal, il est possible d'obtenir algébriquement le temps en fonction de la distance parcourue :
|
|
|
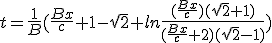
|
|
|
|
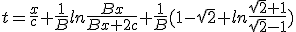
|
| (1.14) |
|
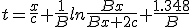
|
Le graphique ci dessous montre la durée en fonction du de la distance, t(x). Évidemment la courbe n'est valable que pour x ≥ 0.
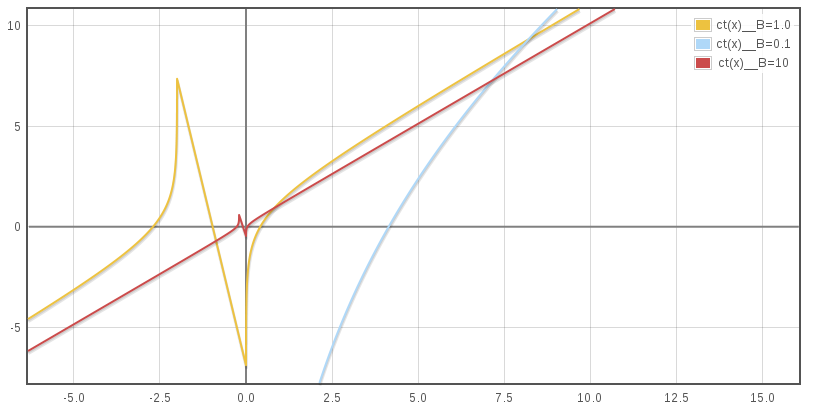
L'asymptote quand x tend vers +∞ de toutes les courbes formées par les valeurs de B est x/c, la droite qui représente la vitesse de la lumière. En effet, dans (1.14) le reste tend vers 1.348/B. Le décalage serait l'avance concédé au vaisseau ayant un B différent après une course infinie qui aurait démarrée depuis un temps infini avec les deux concurrents immobiles dans un milieu parfaitement homogène.
Le mouvement du Bussard Ramjet parfait est maintenant complètement résolu dans dans son propre référentiel ainsi que dans le référentiel de la matière capturée, que l'on peut assimiler au référentiel de la Terre.
Le mouvement du Bussard Ramjet idéal dans les basses vitesses est, d'après le résultat (1.11), au mieux, exponentiel. Il est clair qu'il a besoin d'une vitesse initiale par rapport à son milieu pour démarrer. Il ne sera sans doute pas suffisant à lui tout seul pour assurer la propulsion.
En revanche, à très grande vitesse son accélération tend vers B/2 quand τ vers ∞, d'après la limite de (1.8).
A ma
connaissance, c'est à ce jour le seul dispositif théorique qui puisse
prétendre une telle performance. Ce bolide idéal est selon moi en tête
de la course, théorique, à la vitesse de déplacement la plus grande.
Malheureusement toute réalisation du Bussard Ramjet concrète aura des performances très inférieures.
[1] Galactic Matter and Interstellar Flight, Robert W. Bussard; Los Alamos Scientific Laboratory, University of California, Los Alamos, NM. Local mirror.
[2] Investigation of outer space rocket appliances, Konstantin Tsiolkovsky, 1903. Local mirror, Voir aussi Wiki, pour ceux qui ne sont pas russophones.
[3] A note on relativistic rocketry, Acta Astronautica, Shawn Westmoreland, Volume 67, Issues 9-10, November-December 2010, pp. 1248 - 1251. Local mirror.
[4] Are Black Hole Starships Possible ?, Louis Crane, Shawn Westmoreland, 2009. Local mirror.
[5] Is Interstellar Travel Possible ?, Opik, E. J., Irish Astronomical Journal, vol. 6(8), p. 299. Local mirror.
[6] The equation of motion of an interstellar Bussard ramjet, Claude Semay and Bernard Silvestre-Brac, Eur. J. Phys. 26 (2005) 75–83, doi:10.1088/0143-0807/26/1/009. Local mirror.
[7] Short course in special relativity, M. Strovink, Spring 2006, University of California, Berkeley, Local mirror.
Les images des formules mathématiques ont été produites avec mimetex. La plupart des hébergeurs gratuits ne proposant pas les cgi-bin, les formules sont prés-compilées à l'aide de ce script.
Je ne serait arrivé à rien sans les travaux cités en référence, en particulier le cours de mécanique relativité restreinte de UBC [7] et ainsi que l'article de Claude Semay et Bernard Silvestre-Brac [6] qui m'a été très utile.
Également indispensables, j'ai beaucoup user des sites qui proposent d'effectuer les calculs en lignes WolframAlpha et Number Empire, en particulier les intégrations et les graphiques.
|
Hosted by the courtesy of GitHub |
The stars ASAP


 Durée du voyage intersidéral  Résolutions de l'ONU en HTML  Bussard Ramjet 
 |
DWARF : dwarf2xml
 ELF : libelf examples  Code presentation : ctoohtml  |