Hosted by the courtesy of    GitHub

The stars ASAP Durée du voyage intersidéral Résolutions de l'ONU en HTML Bussard Ramjet

DWARF : dwarf2xml ELF : libelf examples Code presentation : ctoohtml

---

---

Translation : Emmanuel Azencot
Author : Emmanuel Azencot
Creation : Fri May  2 16:13:44 CEST 2014
Update: Fri May  2 16:13:44 CEST 2014

Ideal Bussard Ramjet Motion
Other bussards ramjets motion

• Symbols
• Method and common calculations
• The ideal Bussard Ramjet
• Bussard ramjet with lost of kinetic energy
• Bussard ramjet with mass ejection
• Bussard ramjet with compound ejection
• Bussard ramjet Bremsstrahlung

Bussard Ramjet is an idea for interstellar propulsion from Dr Robert Bussard released in 1960 [1]. This kind of rocket collects interstellar material from the surrounding medium and burn it as nuclear propellent. In fact, even if the galactic medium is nearly empty, it is not really empty and even contains around 0.1 to 0.3 protons / cm³ [4].

As Dr Bussard device does not need to carry any fuel since it get its energy from medium and so it is not bounded by this constraint. However, this process raise numerous issues around energy balance, especially regarding to the energy spent in material collection, most likely as electromagnetic fields, compared to the energy provided by this harvested material [5].

Although an actual device could hardly reach relativistic range, if we could ever have technology to do so, most authors drive their calculations in the special relativistic frame.

I spent several months to set up correct motion equation for this device in the special relativistic frame, since my studies are such a long time ago and I wish to avoid this burden to those who will find this page by posting the results I have found in different cases.

I cannot guarantee the exactness of the following as this document have never be reviewed and so there should be several errors lying in. For this reason it would be very unwise of you to take it for correct. So I am very interested in any feedback you may send through email you will easily find on the site.

We will work in the comoving frame, instantaneously at rest relative to the device, as explained in "Short course in special relativity" [7].

Symbols

Method and common calculations

In this part is about general processing and calculations of elements that remain the same across the different cases, as collected matter amount, for example.

We only take into account the dimension of space towards motion, x. This way the spacetime event 4-vectors (ct, x, y, z) as well as all Lorentz transform invariants, simplify to only two dimension and can be simply written (ct, x).

We are first going to asses the 4-vector representing the difference between to events infinitesimally closed in proper time (c(τ +dτ), 0, 0, 0) and (cτ, 0, 0, 0), that is ((c(τ +dτ), 0) -(cτ, 0,)), in order to get the distance traveled in the collected matter rest frame, and finally find the amount of collected material.

Then we will apply continuity equation to energy and impulse in the special relativistic frame.

Collection between τ and τ +dτ :

In all cases studied here, matter collection process remain the same, we can assess its amount here and apply it later.

Between these to instants the rocket dredge an area S in a medium of density ρ. As it move forward of an infinitesimal distance dx, it sweep a volume S dx during proper time dτ.

We want the rocket proper time interval corresponding to (c dτ, 0) in the medium rest frame. According to special relativity, Lorentz transform matrix Λ(β) is the right way when the frames are moving from each other with speed β :

(1.1)

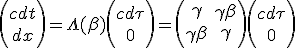
(1.2)

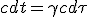
(1.3)

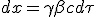
From (1.3) the device covered a distance dx, sweeping a volume S dx in which all the material, at density ρ, is collected : m = ρSdx. We just have to replace dx with (1.3) to have an expression of collected material as a function of time interval :

(1.4)

Momentum at time τ or t :

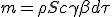
Momentum 4-vector expression as well remain the same for all cases as we do not make assumption on how the collected matter is converted.

Momentum 4-vector of the rocket, having a mass M, in its own rest frame, dropping dimension y and z is :

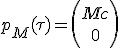
In order to get the momentum of collected interstellar gas we express it in the medium frame and then we change to the rocket frame which have a velocity of -β :

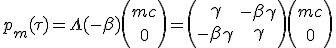
(1.5)

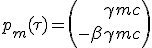
The 4-vector momentum of the system is the sum of the two previous contributions :

(1.6)

Momentum at time just after, τ +dτ :

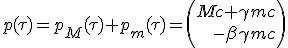
The way the collected material is used will depend on the case study, and thus will be known later. The total energy after conversion, is "e" and the resulting impulse is "q", The collected matter m becomes without loss of generality :

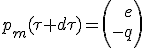
Comparing this result with equation (1.5) we can approximately identify "e" to be γmc. The value of "q" compared to the incoming energy "e" account for device efficiency.

During time interval dτ device speed increase by infinitesimal increment dβ, which give it the new momentum :

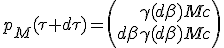
As speed increase dβ is as small as required, we can approximate its Lorentz factor γ(dβ) as being very close from 1. Indeed, at scale of dβ, a second order Tailor development of γ(dβ) give classical mechanic equivalent γ(dβ) ≈ 1 + _½ dβ². As it is a second order of vanishing quantity, we can drop its contribution :

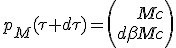
The new system momentum 4-vector at proper time τ +dτ is the sum of its contributors :

(1.7)

Momentum continuity equation :

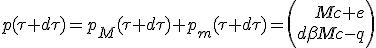
The invariance of momentum 4-vector summarize both impulse and energy conservation :

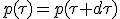
We now split time and space dimension into separate equations :

(E)
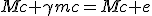
(P)

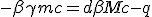
Having still collected material expression at (1.4) :

(1.8)

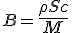
Using value of B with (1.4) and simplifying, we get the general expression of motion :

(M)
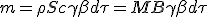
(E)
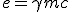
(P)
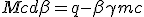
(1.9)

With equation (1.9) and having e and q expression according to collected material conversion we will be able to derive an expression of dβ.

The ideal Bussard Ramjet

This case being simple enough to be fully solve algebraically, it is has its own dedicated separate page. We can check that we find the same differential equation from here.

In this case the overall collected energy is converted to impulse. This mean that all total energy is burned into light emitted exactly in direction -x. It comes then that e = q. With (1.9-E) it turns that q = γmc. Combined with (1.9-P) we obtain :

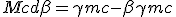
(1.10)

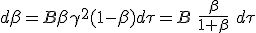
Which happens to be the differential equation found at (1.8).

All devices listed below will be less efficient that Ideal Bussard ramjet.

Bussard ramjet with lost of kinetic energy

It is a simple case where the overall collected matter is burned into light sent towards -x axis, but where the kinetic energy of collected material is completely lost.

If kinetic energy is lost, then mass energy is the only available contribution to linear momentum. Then as mass energy conversion is assumed to be loss less, we have q = mc. Having expression of q we can use it in equation (1.9-P):

(1.11)

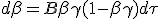
Terminal velocity :

Integration :

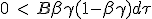
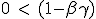
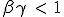
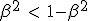
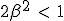
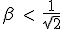
As β is not an additive parameter, we make a variable substitution from β to boost, η(β) = η = atanh(β) which is additive, to be able to integrate. As the derivative of tanh(x) at x = 0 is 1, we can simply replace dβ with dη. From Forward-inverse trigonometric formulae it come than γ = cosh(η) and βγ = sinh(η). The equation (1.11) becomes:

Both WolframAlpha and Number Empire give an expression for the integration.

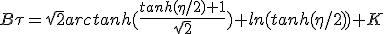
Unfortunately, it is quite complex and inverting it to derive an expression of β as a function of τ is too difficult and we will not go further.

Bussard ramjet with mass ejection

In this device the total collected energy is converted into matter exhaust towards -x axis. A part, ε, of collected material is released into kinetic energy for to the remaining material.

The total energy outgoing flow, e, can be expressed as the energy of the remaining materiel (1 -ε)mc, with its new speed, -ω. The equation (1.9-E) thus turn to :

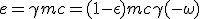
In order to use (1.9-P), we need now q which is derived in the same way as energy :

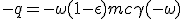
We note that q = e ω = γmc ω. We are only missing an expression of ω we can extract from energy :

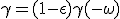
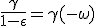
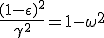
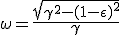
We can now replace this value of ω into the expression of q found previously :

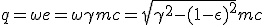
We feed this expression of q in the impulse continuity equation (1.9-P) to get the speed differential equation. Then we replace m by its value given at (1.9-M) :

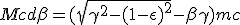
(1.12)

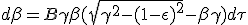
The equation (1.12) is indeed equivalent to the differential equation found in (15), for the same case studied by Claude Semay and Bernard Silvestre-Brac in [6]. Their calculations have been driven starting from collected matter rest frame and later brought to the rocket rest frame :

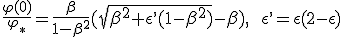
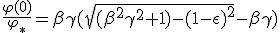
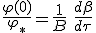
To integrate the differential equation, there is an algebraic solution, we separate terms containing β and γ on left hand side and time on right, then we make variable substitution towards η :

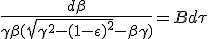
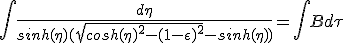
An expression of the integral is provided by WolframAlpha.

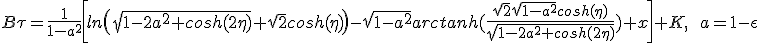
Once again it will be very difficult to invert the function τ(η) to get η(τ) and then β(τ).

Terminal velocity :

According to (1.12), dβ is positive as long as :

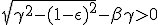
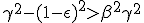
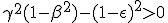
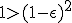
As the inequality leads to an obvious true fact, it is always true. This device has no terminal velocity.

Bussard ramjet with compound ejection

This model is based on the one used in [3] as a model of matter-antimatter engine. The exhaust is a mix of boosted matter, light and loss.

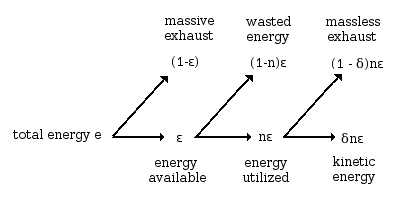
The engine convert a part ε of collected energy flow into energy available for utilization. The remaining (1 -ε) part is thrown out in -x direction. From the useful part ε, a fraction (1 -n) of the energy is wasted most likely through isotropic radiation. The remaining energy, nε, is again partitioned into a δ part as a massless exhaust towards -x direction and (1 -δ) fraction as kinetic energy of the massive exhaust particles.

Below we summarize the distribution of total collected energy into exhaust partition by matter flow, loss and massless particles :

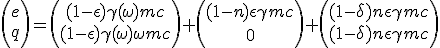
Evry quantities related to q being negative as exhaust are directed to -x, we have simplified to the opposite.

Total incoming energy still being e = γmc, we can derive exhaust massive particles speed ω :

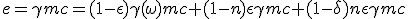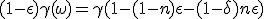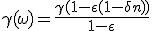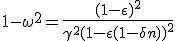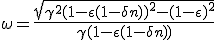Knowing ω it is straightforward to get q and then dβ with (1.9-P) and (1.9-M) :

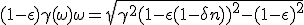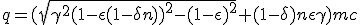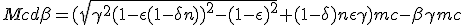
(1.13)

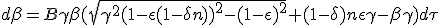
In order to derive an expression of β from the previous differential equation one can proceed as shown before, grouping terms containing β and γ on one side and terms containing proper time on the other. Then apply variable substitution of β and γ to boost η.

Terminal velocity : :

According to (1.13), dβ stay above zero until :

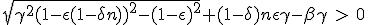
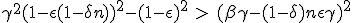
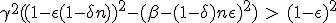
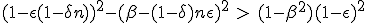
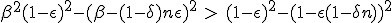
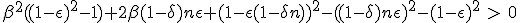
This is a second order equation for β, which may indicates that there is a speed limit. We do not go further in the resolution, as this will be very tedious.

Bussard ramjet Bremsstrahlung

So far it was assumed that the collected matter was used in its own rest frame. But as speed increase, the on-board transit time of particle will become too small to allow any interaction with the rocket.

Now the collected matter is first going to be slow down at the same speed as the rocket. We assume that this deceleration produce a braking radiation emitted strait away towards -x direction with an amount of energy corresponding to the incoming kinetic energy. The physical phenomena which is close from is the Bremsstrahlung radiation, which is considered as a major concern for bussard ramjet [8].

We assume that the part of kinetic energy successfully re-emitted as massless exhaust is t. The part (1 -t) is lost. Collected matter, now stationary from the rocket is converted in a massless flow towards -x. Recalling that kinetic energy of massive particle is (1-γ)mc :

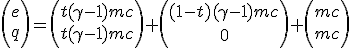
Energy equation is useless as it fully simplify. Never mind, we only need q to complement (1.9-M) :

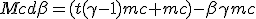
(1.14)

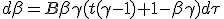
If we assume t = 1, then one can check he finds the ideal bussard given at (1.10). Similarly, if we take t = 0, we find the bussard with loss of kinetic energy given at (1.11).

Integration is as usual, grouping terms and variable substitution towards boost.

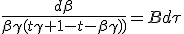
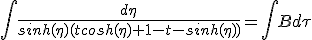
Terminal velocity :

According to (1.14), dβ is positive if :

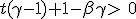
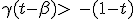
From this we can state that terminal velocity is at least greater than t.c where t is the part of kinetic energy transferred. We now looking to the roots of equation :

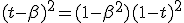
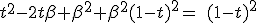
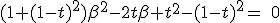
Which happens to be a second order equation with β.

Which solution is in our reach :

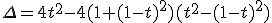
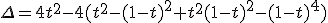
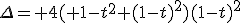
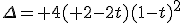
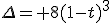
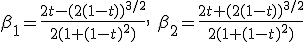
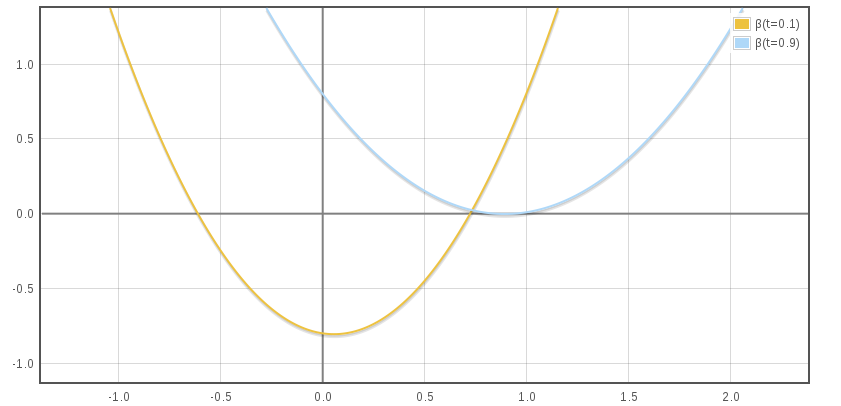
Terminal velocity is given by β₂ which is always positive. This correspond to the limit speeds found from the bussard with kinetic energy lost (β_max = 1/√2) for t = 0, and ideal bussard (β_max = 1) for t = 1.

We can plot the graph of β_max as a function of kinetic energy transfer rate t :

Conclusion

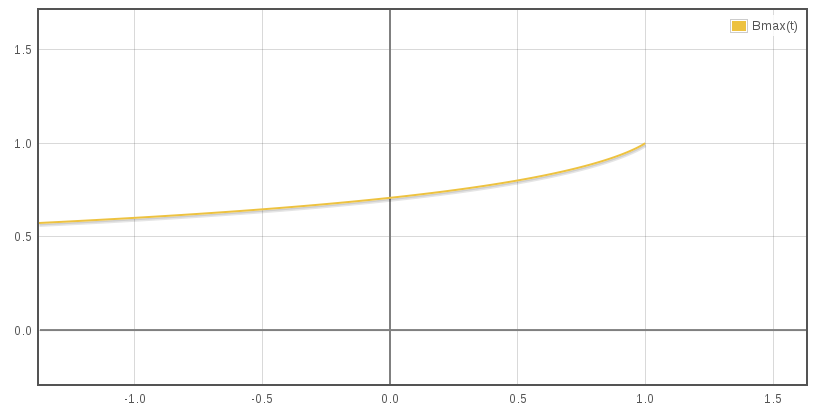
Rather simple in the ideal case, the motion of bussards very quickly gets heavier as soon as inefficiency is taken into account. On most cases, the expression of β as a function of τ, obtained after integration, is not invertible which make next steps difficult.

All those devices assume that matter collection, through the B constant, is simple and at no cost, which will certainly not be true for a real device. The study of matter collectors taking into account required electromagnetic fields and their efficiency would be very interesting but surpasses my skills.

References

[1] Galactic Matter and Interstellar Flight, Robert W. Bussard; Los Alamos Scientific Laboratory, University of California, Los Alamos, NM. Local mirror.
[2] Investigation of outer space rocket appliances, Konstantin Tsiolkovsky, 1903. Local mirror, See also Wiki, if one do not read russian.
[3] A note on relativistic rocketry, Acta Astronautica, Shawn Westmoreland, Volume 67, Issues 9-10, November-December 2010, pp. 1248 - 1251. Local mirror.
[4] Our Local Galactic Neighborhood, Dr. Paulett Liewer. Gives a density around ~0.3 atoms/cm³. Cette autre reférence Local Chimney and Superbubbles is more exhaustive about local bubble medium.
[5] Is Interstellar Travel Possible ?, Opik, E. J., Irish Astronomical Journal, vol. 6(8), p. 299. Local mirror.
[6] The equation of motion of an interstellar Bussard ramjet, Claude Semay and Bernard Silvestre-Brac, Eur. J. Phys. 26 (2005) 75–83, doi:10.1088/0143-0807/26/1/009. Local mirror.
[7] Short course in special relativity, M. Strovink, Spring 2006, University of California, Berkeley, Local mirror.
[8] Bremmstrahlung radiation losses in polywell^tm systems, Robert W. Bussard and Katherine E. King, Oct 1992, .

Acknowledgments

Mathematical image were produced with mimetex. Most of free web hosting do not provided arbitrary binary cgi-bin, formulas have been processed with this especially crafted script.

Reading the works quoted as reference has been a great help for this little work, particularly the Short course in special relativity of M. Strovink, as the article from Claude Semay and Bernard Silvestre-Brac [6].

I have also make a intensive use online calculation resources as WolframAlpha and Number Empire, especially for integration and graphics.

Hosted by the courtesy of    GitHub

The stars ASAP Durée du voyage intersidéral Résolutions de l'ONU en HTML Bussard Ramjet

DWARF : dwarf2xml ELF : libelf examples Code presentation : ctoohtml